Ever wondered why the black hole in Interstellar looks like two rings intersecting each other orthogonally? It’s because of the gravitational lensing effect.
Physics behind this phenomenon comes from Einstein’s general relativity and is quite complicated. (If you are interested, this Quora post has an in-depth walk-through.) However, There is an important clue that light travels in the same way as a non-zero mass particle does. This means that we can simulate the gravitational lensing effect by simulating the trajectory of a particle in a gravitational field since we don’t have to worry about the speed of light, etc. in this simplified model.
The model starts like ray tracing. We start with a screen and a virtual camera. The screen is divided into a grid of pixels. For each pixel, we shoot a virtual particle from the camera to the pixel. The position of the camera becomes the initial position of the particle. The velocity of the particle is set to be the unit vector pointing from the camera to the pixel.
The particle is then calculated regarding the gravitational field, that is:
\[\vec{F} = m\vec{a} = \sum_{M, \vec{d} \in \text{mass-points}} \frac{GMm}{\vec{d}^2}\hat{d}\]Where $d$ is the distance between the particle and the mass point, $M$ is the mass of the mass point, $m$ is the virtual mass of the particle, $G$ is the gravitational constant, and $\hat{d}$ is the unit vector pointing from the mass point to the particle.
Since $m$ cancels out (the mass of an object doesn’t affect its acceleration in a gravitational field), we can simplify the equation to:
\[\vec{a} = \frac{\mathrm{d}^2 \vec{x}}{\mathrm{d}t^2} = \sum_{M, \vec{d} \in \text{mass-points}} \frac{GM}{\vec{d}^2}\hat{d}\]An analytical solution might exist but it is too complicated to be useful when it comes to calculate the collision of the trajectory and the visible objects.
Instead, we can use a numerical method to solve this equation. The movement of the particle can be calculated in a discrete manner. For each time step $\Delta t$, the model checks if the segment $x(t) \rightarrow x(t+\Delta t)$ bumps into any visible object. If so, the model stops the particle at the point of collision and paints the pixel with the color of the object.
Although the method seems dumb, it actually completes calculation in reasonable time. You can find my implementation glens at GitHub. The software is developed in Rust and outputs images in PPM format.
With a bit of scripting (or meta-scripting?) even videos can be generated.
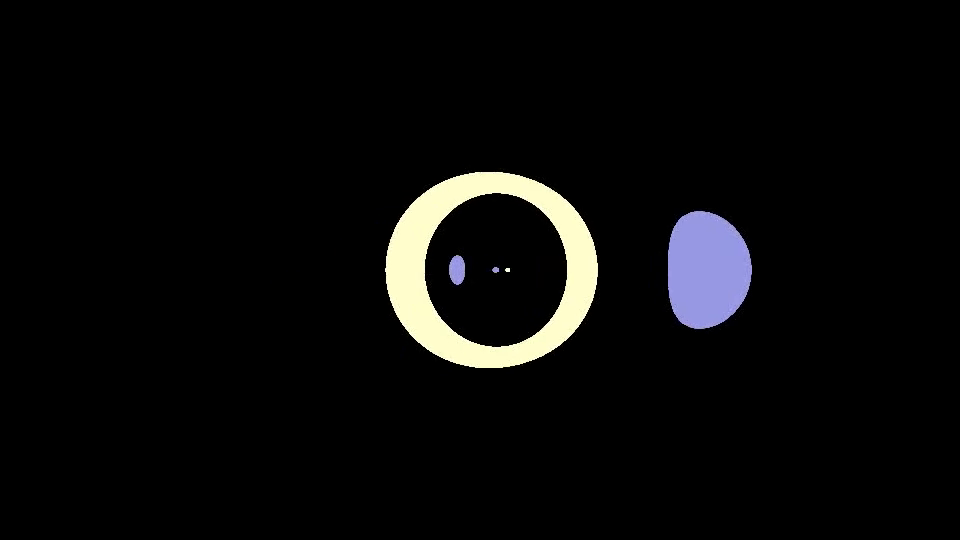
In the video above, an invisible black hole passes two visible stars. The gravitational lensing effect is clearly visible. Stars behind the black hole are distorted and duplicated. For example, in this image:
The yellow star is actually behind the black hole. However, due to the gravitational lensing effect, the light is redirected into a ring (known as the Einstein ring) around the black hole. The left blue star is a duplicated version of the original one. Light is bent by the black hole and redirected to the actual position of the star, passing the back of the black hole.
The video below shows two black holes with accretion disk dancing around each other. The gravitational lensing effect is even more obvious.