人教版的物理必修二中跳过了对匀速圆周运动的向心力的推导,用精确的实验表明,向心力的大小可以表示为...或...这一套模糊的说辞蒙混过关了。这篇文章旨在帮助高中生理解公式的来历。
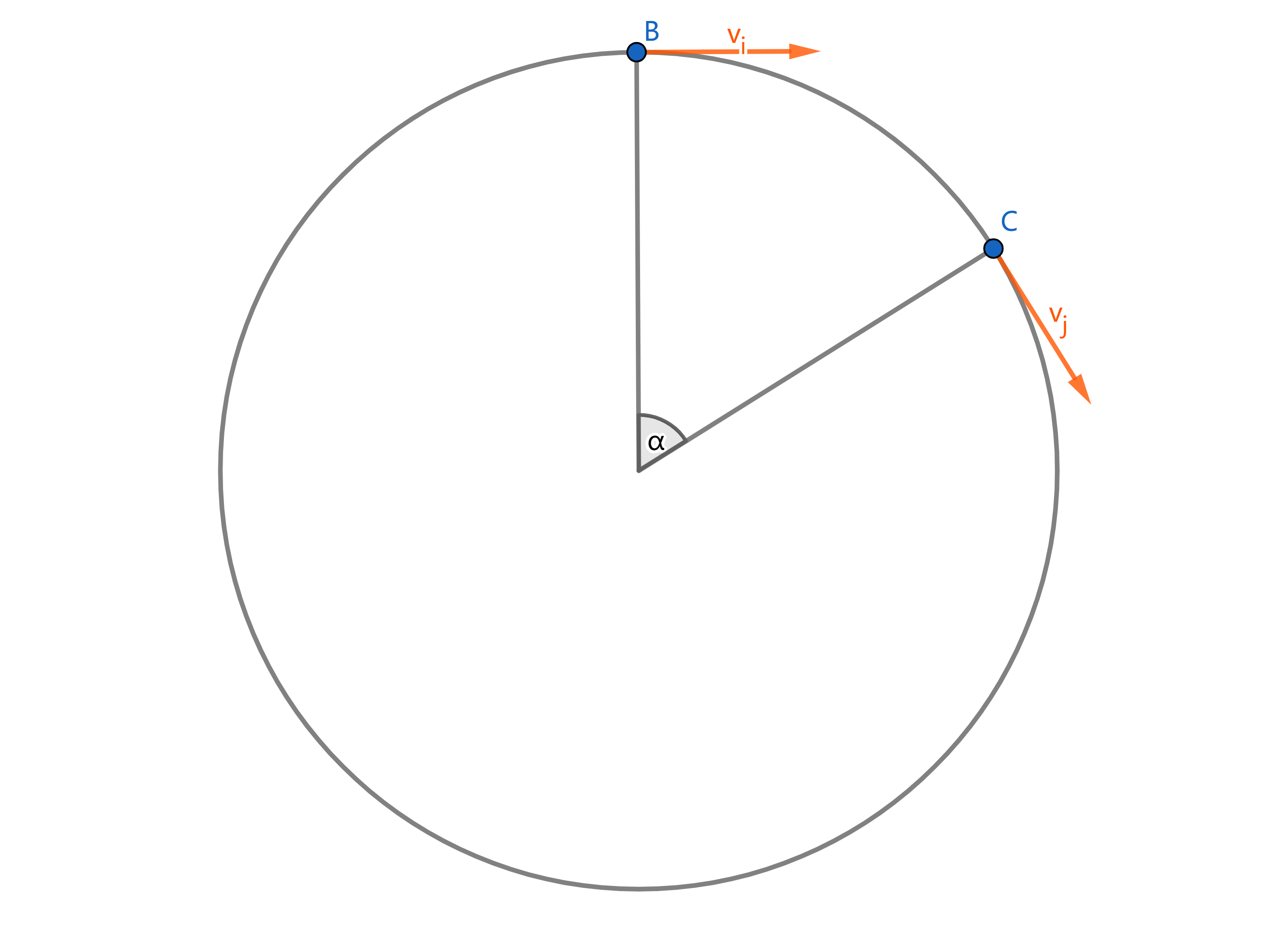
考虑一个物体在圆周上运动。我们记圆周运动的半径为$r$,线速率为$v$,角速度为$\omega$,$0$和$t$时刻的线速度为$\vec{v_{i}}$和$\vec{v_{j}}$,经过的角度为$\alpha$,易知$\lvert \vec{v_{i}} \rvert = \lvert \vec{v_{j}} \rvert = v$,且都与圆相切。
这一段时间中的平均加速度为
\[\vec{a} = \frac{\vec{v_{j}}-\vec{v_{i}}}{t}\]当$t\rightarrow 0$时候$\vec{a}$为瞬时加速度。
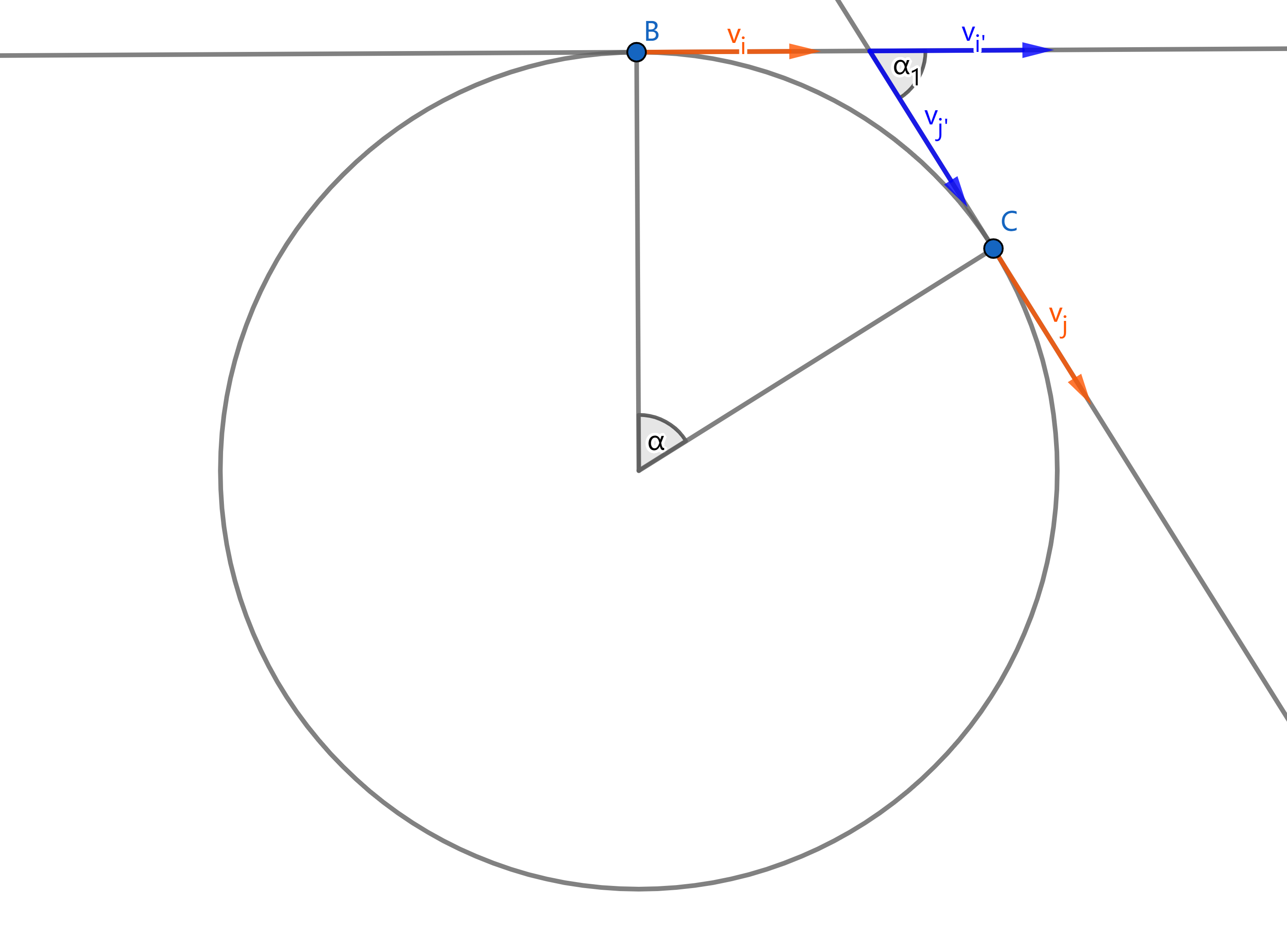
可以看到在式子中我们要将两个向量相减。我们可以通过平移把两个向量尾尾相接便于计算。由切线的性质,可以发现平移后的$\vec{v_{i}’}$和$\vec{v_{j}’}$夹角$\alpha_{1}=\alpha$。
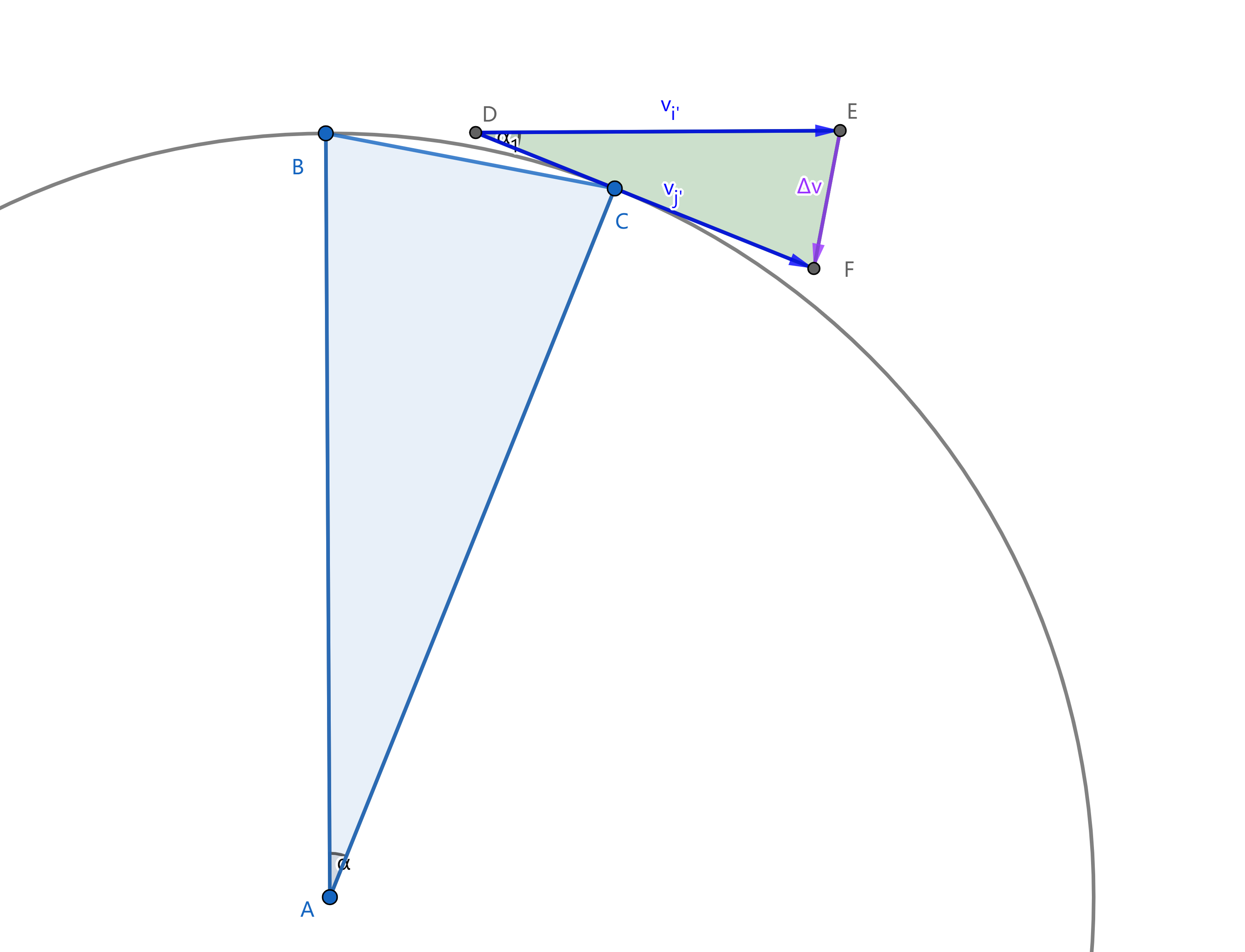
我们可以在图片中画出$\overrightarrow{\triangle v}=\vec{v_{j}’}-\vec{v_{i}’}$。不熟悉向量减法的可以用$\overrightarrow{\triangle v}+\vec{v_{i}’}=\vec{v_{j}’}$思考,即$\vec{v_{i}’}$加上一个向量等于$\vec{v_{j}’}$。
接下来一步至关重要。由于$AB=AC$,$DE=DF$,$\alpha_{1}=\alpha$,可以证明$\triangle ABC \sim \triangle DEF$。所以
\[\frac {\lvert \overrightarrow{\triangle v} \rvert} {\lvert \vec{v_{i}'} \rvert} = \frac {BC} {AB} = \frac {BC} {r}\]由于我们在求解瞬时加速度,$t\rightarrow 0$时$\alpha \rightarrow 0$,$BC \rightarrow \overset{\LARGE\frown}{BC}$,所以
\[\frac {\lvert \overrightarrow{\triangle v} \rvert} {\lvert \vec{v_{i}'} \rvert} = \frac {\overset{\LARGE\frown}{BC}} {r} = \frac {\alpha r} {r} = \alpha\] \[\lvert \overrightarrow{\triangle v} \rvert = \alpha \lvert \vec{v_{i}'} \rvert = \alpha v\]将得到的$\lvert \overrightarrow{\triangle v} \rvert$代入$\vec{a}$,可以求出瞬时加速度的大小
\[\lvert \vec{a} \rvert = \lvert \frac{\vec{v_{j}}-\vec{v_{i}}}{t} \rvert = \frac{\lvert \overrightarrow{\triangle v} \rvert}{t} = \frac{\alpha v}{t}\]由线速度和角速度的定义,可以得到
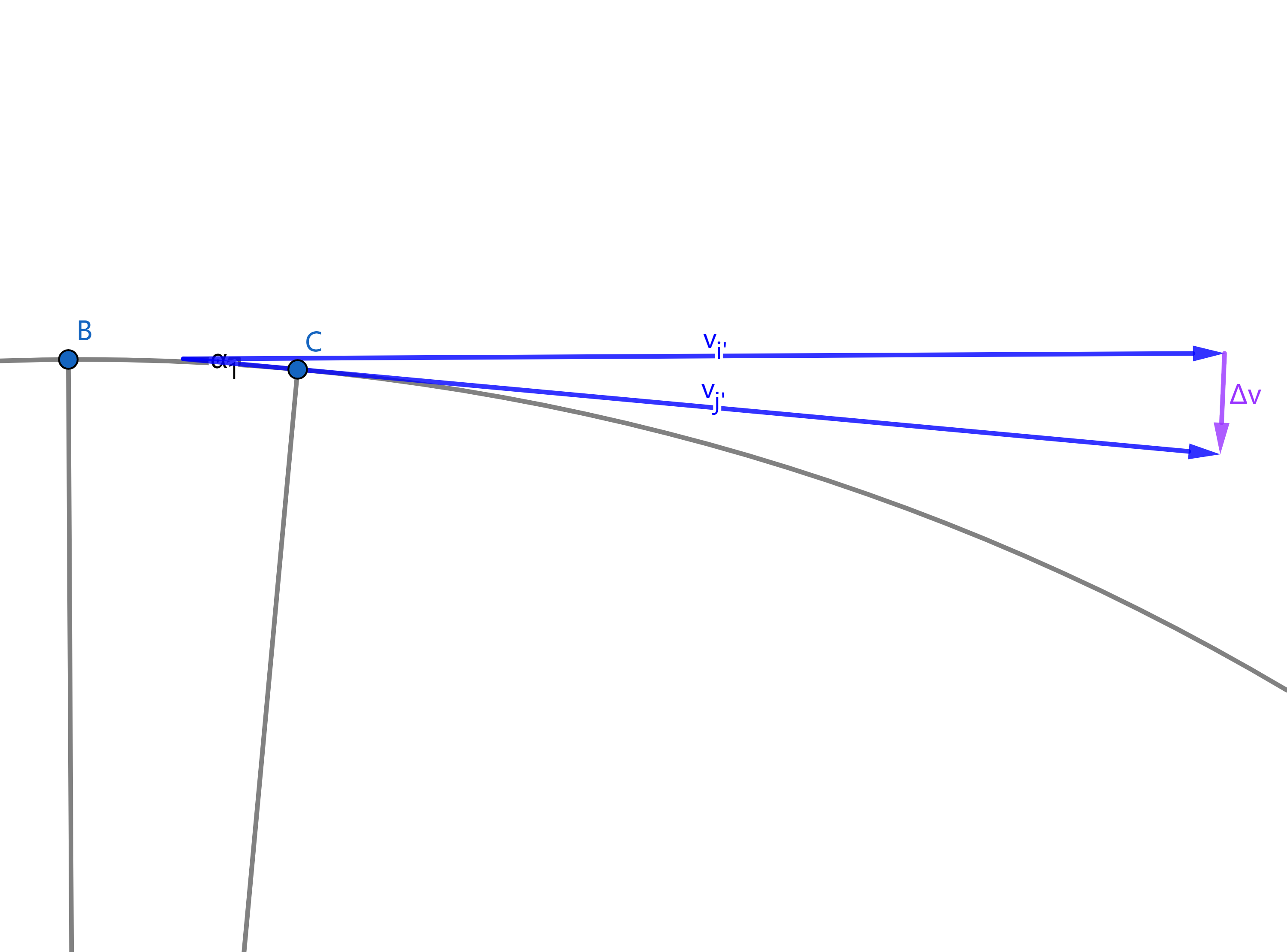
\[\lvert \vec{a} \rvert = v \omega\]但这只是加速度的大小。观察以下图像:
易得当$t \rightarrow 0$时$\alpha_{1} \rightarrow 0$,此时$\overrightarrow{\triangle v}$与圆的切线垂直,即$\vec{a}$朝向圆心。